《工程燃烧学》

 

2024-2025学年第一学期课程实验报告

 

姓    名：         X X X            

 

学    号：       XXXXXXXXX        

 

班    级：         XXXXXXX           

 

主讲教师：          苏福永          

      2024年1月1日

用Matlab对固体和液体燃料温度进行计算

1、问题描述

1.1 语言种类：Matlab

1.2 计算内容：进行理论燃烧温度的近似计算，不考虑分解热。

1.3 计算要求：

（1）具备燃料输入功能（成分范围：固体和液体燃料输入C、H、O、N、S、AM等的质量分数。

（2）具备空气过剩系数输入功能（＞1，混合良好），不考虑热分解。

（3）燃烧产物范围包括：CO、H₂O、CO₂、SO₂、H₂、O₂、N₂ 。

其比热计算方法：

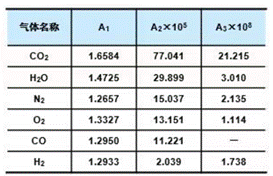
表一：各气体的A1，A2，A3值

（4）采用迭代法进行计算，收敛条件为。不用采用插值法、近似估算等方法。

（5）输出计算后的理论燃烧温度。

 

2，固体和液体燃料t_tc计算原理

2.1反应式：C +O₂ = CO₂ ；H₂ +0.5 O₂ = H₂O ；S + O₂ = SO₂

2.2 为燃烧低位发热量，计算公式为：

2.3 为燃料带入的物理热，计算公式为：，可假设起初燃料未预热，0。

2.4 为空气带入的物理热，计算公式为：

2.5 为实际燃烧产物生成量，计算公式为：

  其中，

2.5 SO₂的A1，A2，A3值的计算：

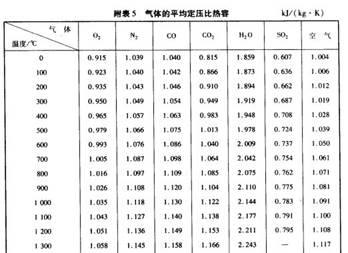
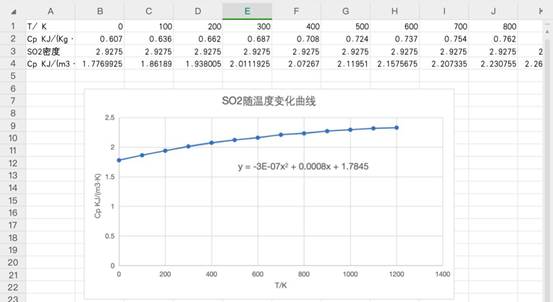
SO₂的A1=1.7845；A2=80；A3=-30

2.6 由上面的表一数据可得比热的计算为：

 

3，Matlab程序代码

clc

clear

%=======参数区输入区域===================

C=input('请输入C的质量分数%=');

H=input('请输入H的质量分数%=');

O=input('请输入O的质量分数%=');

N=input('请输入N的质量分数%=');

S=input('请输入S的质量分数%=');

A=input('请输入A的质量分数%=');

M=input('请输入M的质量分数%=');

a = input(' 请输入空气过剩系数： ');

ta = input(' 请输入空气预热温度(单位℃,环境温度为25℃)： ');

t1=input('请输入假设的理论燃烧温度t1=');

%比热系数，由上到下依次为 CO2 H2O N2 O2 CO H2 CH4

Cp = [1.6584,77.041,21.215;

1.4725,29.899,3.01;

1.2657,15.037,2.135;

1.3327,13.151,1.114;

1.7845,80,-30;];

%========非迭代参数计算区域============

t0 = 25;        %环境温度

Q_net =4.187.*(81.*C+246.*H-26.*(O-S)-6.*M);  %低位发热量

L0=(8.89.*C+26.66.*H+3.33.*S-3.33.*O)./100;     %理论空气需求量

La = a*L0;      %总空气量

Va = (C./12+S./32+H./2+M./18+N./28).*0.224+(a-0.21).*L0;      %实际燃烧产物量

Va_CO2 = C./12.*0.224;     %燃烧产物中CO2的占比

Va_SO2 = S./32.*0.224;     %燃烧产物中SO2的占比

Va_H2O =H./2.*0.224+M./18.*0.224;       %燃烧产物中H2O的占比

Va_N2 = N./28.*0.224+0.79.*La;       %燃烧产物中N2的占比

Va_O2 =0.21.*(a-1).*L0;       %燃烧产物中O2的占比

%=========迭代区==============

T = 0;

T_tc = 6;

Time = 0;

while ( abs(T_tc-T) > 5)

    T = T_tc;

    %比热计算

    Cp_CO2 = Cp(1,1)+ Cp(1,2)*10^(-5)*T_tc + Cp(1,3)*10^(-8)*T_tc^2;

    Cp_H2O = Cp(2,1)+ Cp(2,2)*10^(-5)*T_tc + Cp(2,3)*10^(-8)*T_tc^2;

    Cp_N2 = Cp(3,1)+ Cp(3,2)*10^(-5)*T_tc + Cp(3,3)*10^(-8)*T_tc^2;

    Cp_O2 = Cp(4,1)+ Cp(4,2)*10^(-5)*T_tc + Cp(4,3)*10^(-8)*T_tc^2;

    Cp_SO2 = Cp(5,1)+ Cp(5,2)*10^(-5)*T_tc + Cp(5,3)*10^(-8)*T_tc^2;

    %空气预热

    Cpa=1.004;%查资料所得，空气的比热容Cpa=1.004KJ/(Kg*℃）

    Qa=La.*Cpa.*(ta-t0);

    %产物比热

Cp_Va=(Va_CO2./Va .*Cp_CO2+Va_H2O./Va .*Cp_H2O+Va_N2./Va .*Cp_N2+Va_O2./Va .*Cp_O2+Va_SO2./Va .*Cp_SO2);

    %理论燃烧温度

    T_tc = ( Q_net + Qa ) / ( Va * Cp_Va);

    %计步器

    Time = Time + 1 ;

End

 

4，计算案例

固体和液体燃料理论燃烧温度的近似计算

请输入C的质量分数%=79.1

请输入H的质量分数%=3.3

请输入O的质量分数%=4.2

请输入N的质量分数%=1

请输入S的质量分数%=0.5

请输入A的质量分数%=10.1

请输入M的质量分数%=5.9

请输入空气过剩系数a=

请输入空气预热温度ta/℃=

请输入假设的理论燃烧温度t1=

T_tc=

 

4.1理论燃烧温度与空气过剩系数的关系

燃料种类不变，空气预热温度ta/℃=200不变，假设的理论燃烧温度t1=1100℃不变，只改变空气过剩系数a，由四组数据可得：

当t1=1100℃，ta/℃=250℃，a=1.1时，T_tc= 1798.2℃。

当t1=1100℃，ta/℃=250℃，a=1.2时，T_tc= 1716.9℃。

当t1=1100℃，ta/℃=250℃，a=1.3时，T_tc= 1646.0℃。

当t1=1100℃，ta/℃=250℃，a=1.4时，T_tc=1578.5℃。

  

 

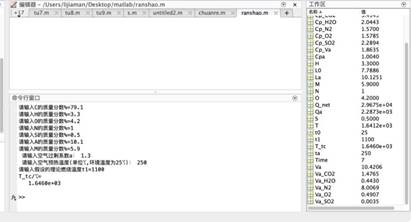
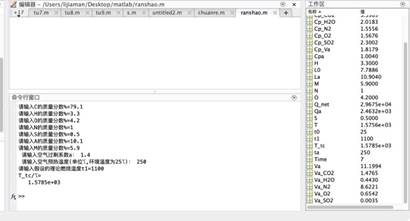
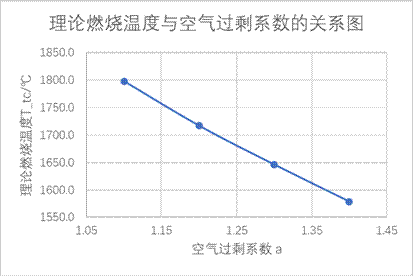
1）以上四组，可见随着空气过剩系数的增加，燃料的理论燃烧温度下降。但由于数据较少，所以无法确定下降趋势是不是线性或非线性的。

4.2理论燃烧温度与空气预热温度的关系

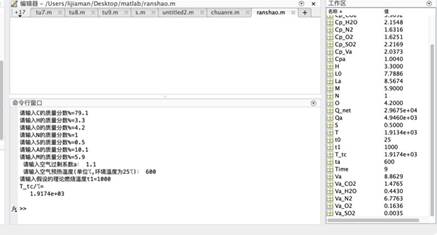
燃料种类不变，空气过剩系数a=1.1不变，假设的理论燃烧温度t1=1000℃不变，只改变空气预热温度，由四组数据可得：

当a=1.1，t1=1000℃，ta/℃=400℃时，T_tc=1849.9℃。

当a=1.1，t1=1000℃，ta/℃=500℃时，T_tc=1883.8℃。

当a=1.1，t1=1000℃，ta/℃=600℃时，T_tc= 1917.4℃。

当a=1.1，t1=1000℃，ta/℃=700℃时，T_tc= 1950.5℃。

 

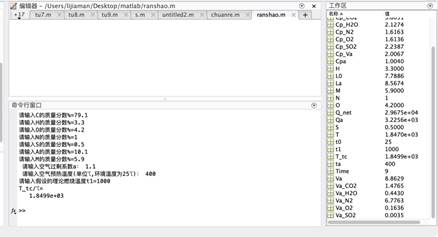
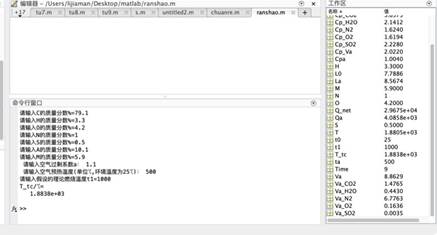
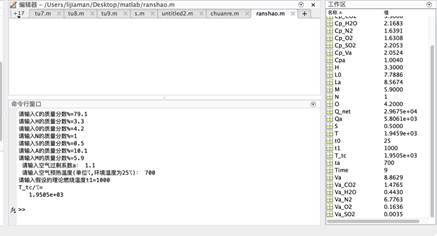
2）以上四组，可见随着空气预热温度的增加，燃料的理论燃烧温度上升。但由于数据较少，所以无法确定上升趋势是不是线性或非线性的。

 

4.3理论燃烧温度与刚开始预设的理论燃烧温度的关系

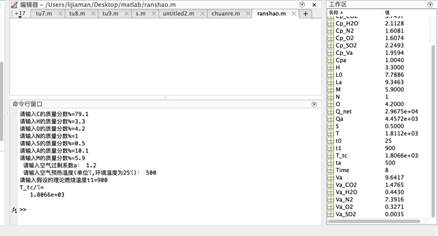
燃料种类不变，空气过剩系数a=1.1不变，空气预热温度ta/℃=500不变，只改变假设的理论燃烧温度t1，由四组数据可得：

当a=1.2，ta/℃=500℃，t1=800℃时，T_tc=1806.6℃

当a=1.2，ta/℃=500℃，t1=900℃时，T_tc=1806.6℃

当a=1.2，ta/℃=500℃，t1=1000℃时，T_tc=1806.6℃

当a=1.2，ta/℃=500℃，t1=1100℃时，T_tc=1806.6℃

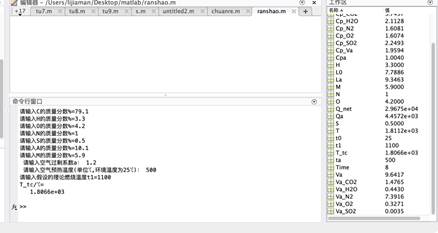
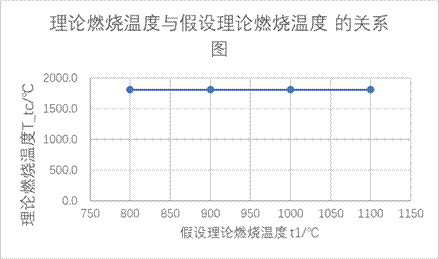
3）以上四组，可见随着刚开始预设的理论燃烧温度的增加，燃料的理论燃烧温度保持不变。

 

4.4理论燃烧温度还与燃料种类，燃烧速度，燃料预热温度等等有关。